当前位置 博文首页 > Inmaturity_7的博客：算法练习帖--57--保证图可完全遍历(Java)
Alice 和 Bob 共有一个无向图，其中包含 n 个节点和 3 种类型的边：
类型 1：只能由 Alice 遍历。
类型 2：只能由 Bob 遍历。
类型 3：Alice 和 Bob 都可以遍历。
给你一个数组 edges ，其中 edges[i] = [typei, ui, vi] 表示节点 ui 和 vi 之间存在类型为 typei 的双向边。请你在保证图仍能够被 Alice和 Bob 完全遍历的前提下，找出可以删除的最大边数。如果从任何节点开始，Alice 和 Bob 都可以到达所有其他节点，则认为图是可以完全遍历的。
返回可以删除的最大边数，如果 Alice 和 Bob 无法完全遍历图，则返回 -1 。
（题目来源：力扣（LeetCode））
示例 1：
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
输出：2
解释：如果删除 [1,1,2] 和 [1,1,3] 这两条边，Alice 和 Bob 仍然可以完全遍历这个图。再删除任何其他的边都无法保证图可以完全遍历。所以可以删除的最大边数是 2 。
示例 2：
输入：n = 4, edges = [[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
输出：0
解释：注意，删除任何一条边都会使 Alice 和 Bob 无法完全遍历这个图。
示例 3：
输入：n = 4, edges = [[3,2,3],[1,1,2],[2,3,4]]
输出：-1
解释：在当前图中，Alice 无法从其他节点到达节点 4 。类似地，Bob 也不能达到节点 1 。因此，图无法完全遍历。
提示：
1 <= n <= 10^5
1 <= edges.length <= min(10^5, 3 * n * (n-1) / 2)
edges[i].length == 3
1 <= edges[i][0] <= 3
1 <= edges[i][1] < edges[i][2] <= n
所有元组 (typei, ui, vi) 互不相同
1. 并查集
package com.lxf.bcj;
class Solution {
public static void main(String[] args) {
Solution solution = new Solution();
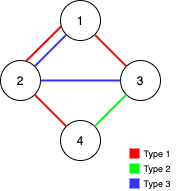
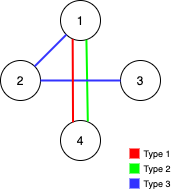
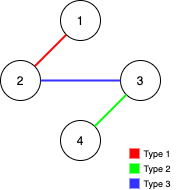
int[][] ints = {{1, 1, 2}, {2, 1, 3}, {3, 2, 4}, {3, 2, 5}, {1, 2, 6}, {3, 6, 7}, {3, 7, 8}, {3, 6, 9}, {3, 4, 10}, {2, 3, 11}, {1, 5, 12}, {3, 3, 13}, {2, 1, 10}, {2, 6, 11}, {3, 5, 13}, {1, 9, 12}, {1, 6, 8}, {3, 6, 13}, {2, 1, 4}, {1, 1, 13}, {2, 9, 10}, {2, 1, 6}, {2, 10, 13}, {2, 2, 9}, {3, 4, 12}, {2, 4, 7}, {1, 1, 10}, {1, 3, 7}, {1, 7, 11}, {3, 3, 12}, {2, 4, 8}, {3, 8, 9}, {1, 9, 13}, {2, 4, 10}, {1, 6, 9}, {3, 10, 13}, {1, 7, 10}, {1, 1, 11}, {2, 4, 9}, {3, 5, 11}, {3, 2, 6}, {2, 1, 5}, {2, 5, 11}, {2, 1, 7}, {2, 3, 8}, {2, 8, 9}, {3, 4, 13}, {3, 3, 8}, {3, 3, 11}, {2, 9, 11}, {3, 1, 8}, {2, 1, 8}, {3, 8, 13}, {2, 10, 11}, {3, 1, 5}, {1, 10, 11}, {1, 7, 12}, {2, 3, 5}, {3, 1, 13}, {2, 4, 11}, {2, 3, 9}, {2, 6, 9}, {2, 1, 13}, {3, 1, 12}, {2, 7, 8}, {2, 5, 6}, {3, 1, 9}, {1, 5, 10}, {3, 2, 13}, {2, 3, 6}, {2, 2, 10}, {3, 4, 11}, {1, 4, 13}, {3, 5, 10}, {1, 4, 10}, {1, 1, 8}, {3, 3, 4}, {2, 4, 6}, {2, 7, 11}, {2, 7, 10}, {2, 3, 12}, {3, 7, 11}, {3, 9, 10}, {2, 11, 13}, {1, 1, 12}, {2, 10, 12},
