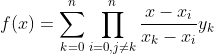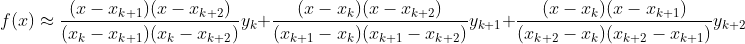插值:已知一些位置的函数值,来推导其余位置的函数值。分为内插interpolation与外推extropolation
一些公式太常见或太复杂则没有附上
插值公式
不等距节点插值公式(差商插值多项式)
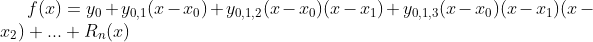
等距节点插值公式(差分公式)
牛顿第一插值公式
节点?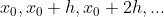
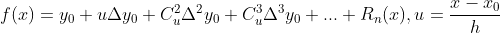
二项式系数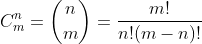
适用于:插值区间起始点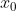 附近的函数值
附近的函数值
牛顿第二插值公式
节点?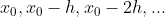
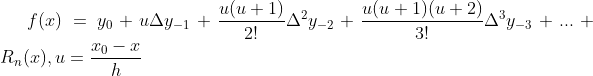
适用于:插值区间终点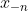 附近的函数值
附近的函数值
斯特林插值公式
适用于插值区间中点附近的函数值
贝塞尔插值公式
适用于两相邻节点之间的中间附近的函数值
拉格朗日插值公式
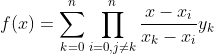
如果节点等距

三次样条插值公式
样条spline
如果满足:S(x)在每个区间上是一个三次多项式,S(x)过所有点,S(x)一阶导与二阶导连续,则称S(x)为过n个点的三次样条函数。
其他插值公式
一元三点插值公式:由最靠近x的三点得出f(x)
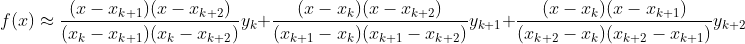
二元插值公式
Hermite插值公式:通过已知的函数值与导数值插值
函数逼近>有理函数逼近>帕德逼近。(有理函数:多项式除法的商)
有限元位移插值,有限体积法场量插值
龙格现象与吉布斯现象
龙格现象:是在一组等间插值点上使用具有高次多项式的多项式插值时出现的区间边缘处的振荡问题,表明使用高次多项式插值并不总能提高准确性。
吉布斯现象:当选取的傅里叶级数的项数N增加时,合成的波形虽然更逼近原函数,但在不连续点附近会出现一个固定高度的过冲,N越大,过冲的最大值越靠近不连续点,但其峰值并不下降,而是大约等于原函数在不连续点处跳变值的9%,且在不连续点两侧呈现衰减振荡的形式。
过冲overshoot:第一个峰值或谷值超过设定电压;下冲undershoot:overshoot:第二个峰值或谷值超过设定电压。
径向基函数RBF
https://www.cnblogs.com/pinking/p/9349695.html
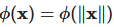
径向基函数的自变量为输入的范数
RBF神经网络:激活函数为径向基函数
RBF核函数:支持向量机的一种核函数

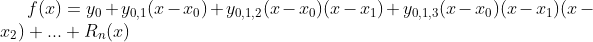
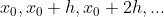
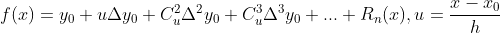
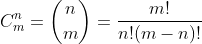
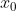 附近的函数值
附近的函数值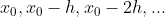
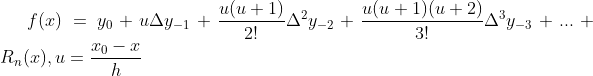
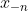 附近的函数值
附近的函数值