-
爱站内页反链
爱站首页反链
神马是否收录
360网站安全检测
搜狗是否收录
360是否收录
百度是否收录
百度年收录
网站年龄
百度安全
百度查询
导出链接
网站ip查询
网站ICP备案批量查询
搜狗快照
百度快照
百度反链批量查询
搜狗PR批量查询
谷歌PR批量查询
神马权重批量查询
360移动权重批量查询
站长移动权重批量查询
爱站移动权重批量查询
360权重查询
站长PC权重批量查询
爱站PC权重批量查询
搜狗总收录批量查询
360日收录批量查询
360总收录批量查询
百度月收录批量查询
百度周收录批量查询
百度日收录批量查询
百度网站收录批量查询
获取网站IP
获取网站描述
获取网站关键词
获取网站标题
HTTP状态码
搜狗权重
搜狗反链
神马总收录
百度预计流量
ALEXA排名
360反链

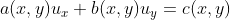
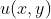 ,由
,由 绘制曲面S
绘制曲面S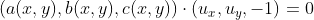
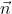 为
为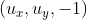
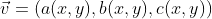 与法向量垂直,向量
与法向量垂直,向量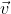 位于曲面S的切平面内
位于曲面S的切平面内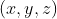 处的切平面都有一个向量
处的切平面都有一个向量
 ,称为特征方程
,称为特征方程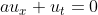
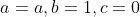
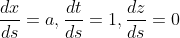
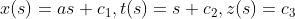

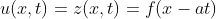
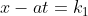 的方向,
的方向,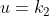 。
。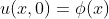
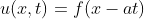
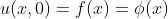 ,即映射
,即映射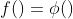
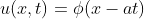
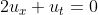 ,
,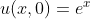
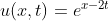
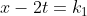


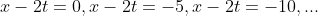 这些平面(相对于x,t,u来说)与积分面的交线为一个等值线
这些平面(相对于x,t,u来说)与积分面的交线为一个等值线
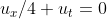 ,
,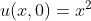
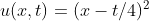
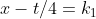
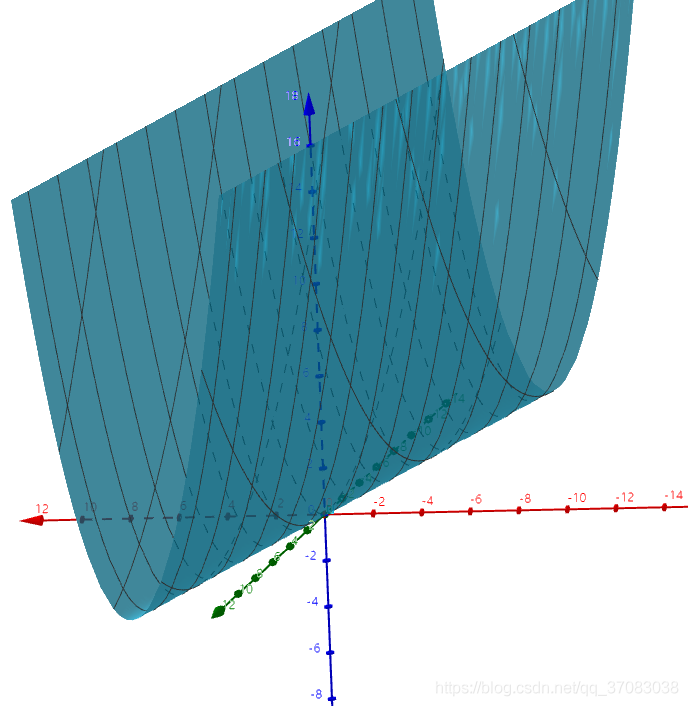
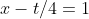 与积分面的交线为一条等值线
与积分面的交线为一条等值线

