流体力学:如何构建pde,cfd:如何求解pde,cfd可看作流体力学的一个分支。
两个期刊:Journal of Fluid Mechanics、Journal of Computational Physics。
学生光会操作商业软件是不行的。
描述流体运动的两种方法
拉格朗日法、欧拉法
研究风速,在固定点安装风速仪,在气球上安装风速仪。
研究某一固定点经过的所有质点,研究某一质点,这都可以研究流体。
前者是欧拉法,后者是拉个格朗日法。
质点导数
质点导数:质点的物理量Φ对于时间的变化率
拉格朗日法质点导数:![[\frac{\partial y }{\partial t}]_L](http://style.iis7.com/uploads/2021/06/1706233545.gif)
欧拉法质点导数:![[\frac{\partial y }{\partial t} + u\cdot \triangledown y]_E](http://style.iis7.com/uploads/2021/06/1706243546.gif)
![[\frac{\partial y }{\partial t} + u\cdot \triangledown y]_E = [\frac{\partial y }{\partial t}]_L](http://style.iis7.com/uploads/2021/06/1706253547.gif)
全导数只是针对欧拉法定义的,在拉格朗日法中,某一质点物理量变化率就是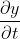 ,在欧拉法中,某一质点物理量变化率为全导数
,在欧拉法中,某一质点物理量变化率为全导数
也称:
advective derivative?平流导数
convective derivative?对流导数
derivative following the motion 随体导数
hydrodynamic derivative?流体动力导数
lagrangian derivative?拉格朗日导数
particle derivative 质点导数
substantial derivative?实质导数
substantive derivative?实质导数
Stokes derivative?斯托克斯导数
total derivative?全导数
任何宏观张量场y=y(x,t)其物质导数为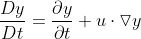
标量场与矢量场

NS方程组
1为连续性方程,2为动量方程

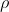 为0阶张量—标量,U为1阶张量—向量
为0阶张量—标量,U为1阶张量—向量
UU为2阶张量—矩阵,
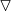 为1阶张量—向量
为1阶张量—向量
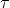 为二阶张量—矩阵
为二阶张量—矩阵
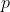 为0阶张量—标量
为0阶张量—标量
所以两个方程写成分量形式为六个方程。
从有限控制体推导的方程为积分形式,分为空间位置固定的有限控制体、随流线运动的有限控制体。若采用空间位置固定的控制体,方程为守恒型方程。若采用随流线运动的控制体,方程为非守恒型。
从无穷小微团推导出来的方程为微分形式,分为空间位置固定的无穷小微团、随流线运动的无穷小微团。
积分形式的方程和微分形式的方程有重要的区别。积分形式的方程可在控制体内出现间断。因为数学上并没有要求被积分的函数不能出现间断。但微分形式的方程要求函数是连续的,否则不可导。
强度量、广延量
intensive quantity、extensive quantity
强度量:与物质的数量无关的量
广度量:与物质的数量有关的量
全导数
全导数 = 局部导数 + 对流导数
根据守恒列方程
连续性方程——质量守恒定律
动量方程——牛顿第二定律
能量方程——能量守恒定律
张量积
也称外积

Nabla算子

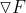 为梯度。矢量函数F,
为梯度。矢量函数F,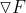 为二阶张量,标量函数F,
为二阶张量,标量函数F,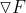 为一阶张量。
为一阶张量。
矢量函数F,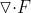 为散度,
为散度,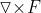 为旋度。
为旋度。
连续性方程
欧拉法
微分形式的连续性方程

积分形式的连续性方程

拉格朗日法


通量、散度
通量 flux:
热学与流体力学中单位时间内通过单位面积的具有方向的流量(向量)
电磁学中单位面积上垂直于其表面的磁场或电场的强度(标量)
体积通量:速度矢量与面矢量的内积
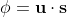 ?
?
速度散度:单位体积流动着的控制体体积随时间的变化率

散度divergence
动量方程
表面力:作用在流体微团面上,压力、表面张力
体积力:作用在流体微团面上与体内,重力、惯性力
应力、压强
应力:物体(表面与内部)单位面积承受的力,正应力与剪应力
压强:物体表面单位面积法向分量的力,压强为正应力
正应力使得物体压缩或膨胀;剪应力使得物体变形,剪应力与形变速率成正比,流体受剪应力主要表现为流体粘性。
非守恒

守恒
连续性方程+非守恒动量方程 推出 守恒动量方程

本构关系
本构关系:剪应力与形变速率的关系(固体力学:应力与应变的关系)
形变率、剪应力是二阶张量
剪应力——形变率——速度

不可压缩流体

可压缩流体

将本构关系带入动量方程,此时动量方程才是封闭的
不可压缩流体
 ?也可写作
?也可写作 (第二种形式只针对不可压缩流体)
(第二种形式只针对不可压缩流体)
可压缩流体

湍流
1877年——1955年
Reynolds:时间平均
Boussinesq:涡粘
Prandtl:边界层;用混合长湍流模型(零方程湍流模型)计算湍流粘度;考虑湍流动能,一方程湍流模型
Kolmogorov:考虑了湍流动能k与能量耗散w,关于k与w的PDE,两方程湍流模型
Rotta:二阶矩湍流模型(雷诺应力传输模型)
目前湍流的数值研究方法主要有:DNS、LES、RANS
湍流模型:Spalart-Allmaras湍流,K-ω湍流,k-ε湍流和SST模型
DNS
Kolmogoroff尺度
主要是有限差分法、谱方法
术语:
网格尺度
粘性尺度
一阶迎风格式
无反射边界条件
无滑移边界条件
LES
湍流中的大涡往往比小涡更具有能量
滤波速度filtering velocity
滤波尺度?
大涡模拟认为,尺度大于?就是大涡,尺度小于?就是小涡
模化
亚格子应力Subgrid-Scale Stress
Bousinessq方法
Smagorinsky湍流模型
RANS
稳态的雷诺平均通常采用时间平均法,非稳态的雷诺平均通常采用集合平均法。
Boussinesq 假定将未封闭的湍流应力与湍流粘度联合起来,这样,就把未知量转化为了湍流粘度变
量
Spalart-Allmaras 模型以及 SST 模型
RSM
雷诺应力模型
DES
分离涡模型
二维模拟
目前学术界普遍的看法是:“无三维涡,则无湍流”。“只有在三维的情况下,流体自身的涡旋才能伸展。”但是大量的文献依旧通过二维大涡模拟、甚至二维直接模拟进行相关研究。
结构网格、非结构网格
结构网格思想更偏向于有限差分。有限体积法则不限定于任何网格类型,更适用于非结构网格。
网格节点序号、网格节点与面相连序号
非结构网格通量计算
非结构网格TVD格式范例
动理学方程
N-S 方程并不是描述流动的最底层的形式。更为底层的数学模型为玻尔兹曼方程。。其在不同的领域有不同的称呼。例如在群体平衡模型研究领域,被称之为普适性群体平衡模型,在空气动力学领域被称之为动理学方程,在喷雾燃烧领域被称之为威廉玻尔兹曼方程。
玻尔兹曼方程

f 气体分子速度分布函数
U 气体分子速度
A 受力引起的气体分子加速度
C 碰撞项
麦克斯韦分布

高斯分布

麦克斯韦分布为高斯分布的各向同性形式
矩方程、五矩模型、十矩模型
守恒与非守恒、守恒变量与原始变量
非牛顿流体
牛顿流体:流体的粘度为常数(剪切应力和形变率的比值为定值)
非牛顿流体:流体的粘度与时间和位置有关
参考
https://www.zhihu.com/question/26992291/answer/1448275421
https://zhuanlan.zhihu.com/p/146396629
https://wuli.wiki/online/fluid2.html
无痛苦N-S方程笔记
continuum mechanics连续介质力学
derivative导数
differentiation偏微
covariant derivative共变导数
never say never,嘿嘿嘿。

![[\frac{\partial y }{\partial t}]_L](http://style.iis7.com/uploads/2021/06/1706233545.gif)
![[\frac{\partial y }{\partial t} + u\cdot \triangledown y]_E](http://style.iis7.com/uploads/2021/06/1706243546.gif)
![[\frac{\partial y }{\partial t} + u\cdot \triangledown y]_E = [\frac{\partial y }{\partial t}]_L](http://style.iis7.com/uploads/2021/06/1706253547.gif)
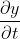 ,在欧拉法中,某一质点物理量变化率为全导数
,在欧拉法中,某一质点物理量变化率为全导数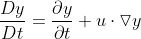


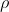 为0阶张量—标量,U为1阶张量—向量
为0阶张量—标量,U为1阶张量—向量
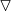 为1阶张量—向量
为1阶张量—向量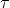 为二阶张量—矩阵
为二阶张量—矩阵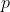 为0阶张量—标量
为0阶张量—标量

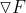 为梯度。矢量函数F,
为梯度。矢量函数F,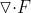 为散度,
为散度,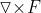 为旋度。
为旋度。

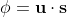 ?
?

 ?也可写作
?也可写作 (第二种形式只针对不可压缩流体)
(第二种形式只针对不可压缩流体)


