当前位置 博文首页 > 韦全敏的博客：从图(Graph)到图卷积(Graph Convolution)：漫谈图
从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (一)
从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (二)
从图(Graph)到图卷积(Graph Convolution)：漫谈图神经网络模型 (三)
在上文中，我们简单介绍了基于循环图神经网络的两种重要模型，在本篇中，我们将着大量笔墨介绍图卷积神经网络中的卷积操作。接下来，我们将首先介绍一下图卷积神经网络的大概框架，借此说明它与基于循环的图神经网络的区别。接着，我们将从头开始为读者介绍卷积的基本概念，以及其在物理模型中的涵义。最后，我们将详细地介绍两种不同的卷积操作，分别为空域卷积和时域卷积，与其对应的经典模型。读者不需有任何信号处理方面的基础，傅里叶变换等概念都会在本文中详细介绍。
在开始正式介绍图卷积之前，我们先花一点篇幅探讨一个问题：为什么研究者们要设计图卷积操作，传统的卷积不能直接用在图上吗？ 要理解这个问题，我们首先要理解能够应用传统卷积的图像(欧式空间)与图(非欧空间)的区别。如果把图像中的每个像素点视作一个结点，如下图左侧所示，一张图片就可以看作一个非常稠密的图；下图右侧则是一个普通的图。阴影部分代表卷积核，左侧是一个传统的卷积核，右侧则是一个图卷积核。卷积代表的含义我们会在后文详细叙述，这里读者可以将其理解为在局部范围内的特征抽取方法。
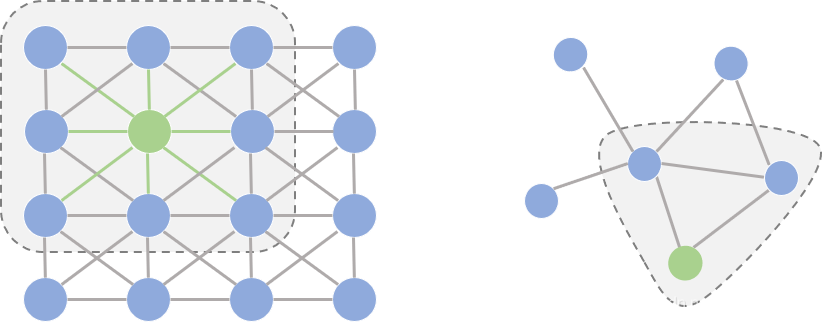
仔细观察两个图的结构，我们可以发现它们之间有2点非常不一样：
真正的难点聚焦于邻居结点数量不固定上。那么，研究者如何解决这个问题呢？其实说来也很简单，目前主流的研究从2条路来解决这件事：
这两条实际上也是后续图卷积神经网络的设计原则，图卷积的本质是想找到适用于图的可学习卷积核。
上面说了图卷积的核心特征，下面我们先来一窥图卷积神经网络的全貌。如下图所示，输入的是整张图，在Convolution Layer 1里，对每个结点的邻居都进行一次卷积操作，并用卷积的结果更新该结点；然后经过激活函数如ReLU，然后再过一层卷积层Convolution Layer 2与一词激活函数；反复上述过程，直到层数达到预期深度。与GNN类似，图卷积神经网络也有一个局部输出函数，用于将结点的状态(包括隐藏状态与结点特征)转换成任务相关的标签，比如水军账号分类，本文中笔者称这种任务为Node-Level的任务；也有一些任务是对整张图进行分类的，比如化合物分类，本文中笔者称这种任务为Graph-Level的任务。卷积操作关心每个结点的隐藏状态如何更新，而对于Graph-Level的任务，它们会在卷积层后加入更多操作。本篇文章主要关心如何在图上做卷积，至于如何从结点信息得到整张图的表示，我们将在下一篇系列文章中讲述。
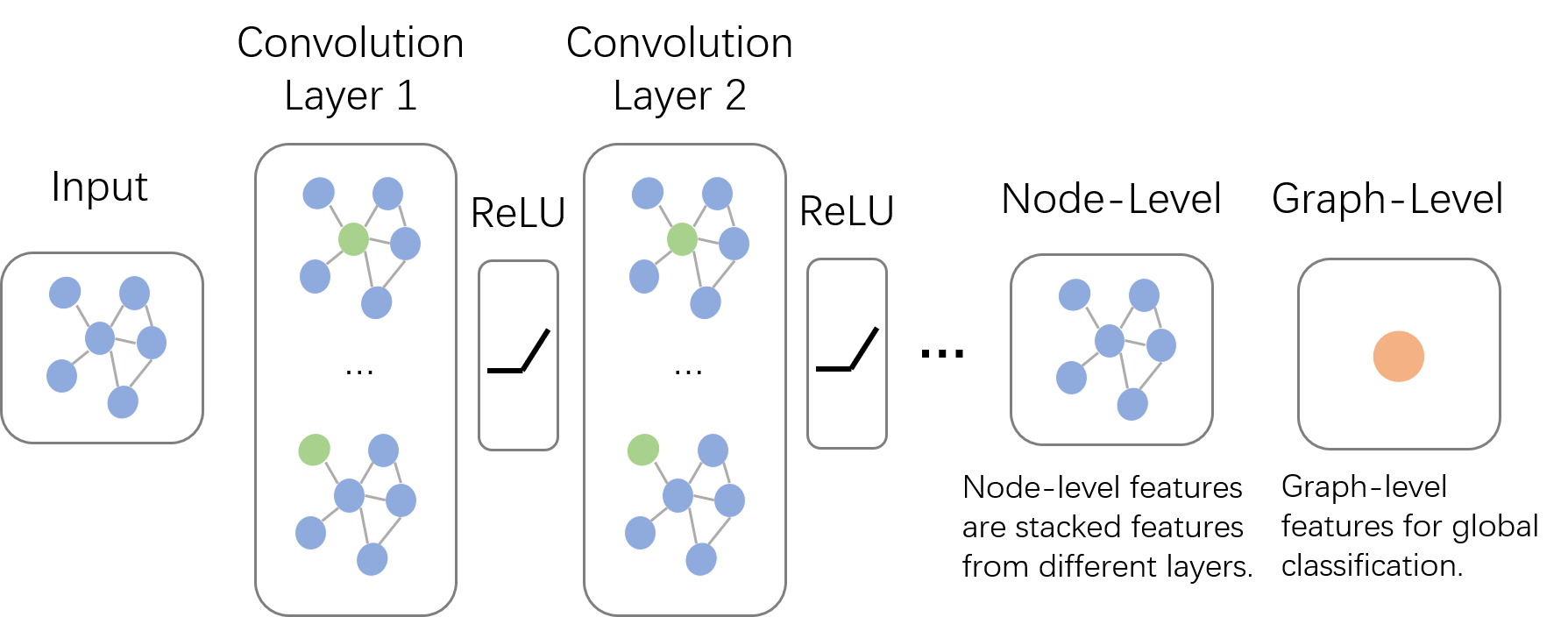
多说一句，GCN与GNN乍看好像还挺像的。为了不让读者误解，在这里我们澄清一下它们根本上的不同：GCN是多层堆叠，比如上图中的Layer 1和Layer 2的参数是不同的；GNN是迭代求解，可以看作每一层Layer参数是共享的。
正如我们在上篇博客的开头说到的，图卷积神经网络主要有两类，一类是基于空域的，另一类则是基于频域的。通俗点解释，空域可以类比到直接在图片的像素点上进行卷积，而频域可以类比到对图片进行傅里叶变换后，再进行卷积。傅里叶变换的概念我们先按下不讲，我们先对两类方法的代表模型做个大概介绍。
基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上，它跟传统的卷积神经网络中的卷积更相似一些。在这个类别中比较有代表性的方法有 Message Passing Neural Networks(MPNN)[1], GraphSage[2], Diffusion Convolution Neural Networks(DCNN)[3], PATCHY-SAN[4]等。
基于频域卷积的方法则从图信号处理起家，包括 Spectral CNN[5], Cheybyshev Spectral CNN(ChebNet)[6], 和 First order of ChebNet(1stChebNet)[7]等。
在介绍这些具体的模型前，先让我们从不同的角度来回顾一下卷积的概念，重新思考一下卷积的本质。
由维基百科的介绍我们可以得知，卷积是一种定义在两个函数( f f f跟 g g g)上的数学操作，旨在产生一个新的函数。那么 f f f和 g g g的卷积就可以写成 f ? g f*g f?g，数学定义如下：
(
f
?
g
)
(
t
)
=
∫
?
∞
∞
f
(
τ
)
g
(
t
?
τ
)
(
连
续
形
式
)
(f*g)(t)={\int}_{-\infty}^{\infty}f(\tau)g(t-\tau) (连续形式)
(f?g)(t)=∫?∞∞?f(τ)g(t?τ)(连续形式)
(
f
?
g
)
(
t
)
=
∑
τ
=
?
∞
∞
f
(
τ
)
g
(
t
?
τ
)
(
离
散
形
式
)
(f*g)(t)={\sum}_{\tau=-\infty}^{\infty}f(\tau)g(t-\tau) (离散形式)
(f?g)(t)=∑τ=?∞∞?f(τ)g(t?τ)(离散形式)
光看数学定义可能会觉得非常抽象，下面我们举一个掷骰子的问题，该实例参考了知乎问题"如何通俗易懂地解释卷积"[8]的回答。
想象我们现在有两个骰子，两个骰子分别是 f f f跟 g g g， f ( 1 ) f(1) f(1)表示骰子 f f f向上一面为数字 1 1 1的概率。同时抛掷这两个骰子1次，它们正面朝上数字和为4的概率是多少呢？相信读者很快就能想出它包含了三种情况，分别是：
最后这三种情况出现的概率和即问题的答案，如果写成公式，就是
∑
τ
=
1
3
f
(
τ
)
g
(
4
?
τ
)
\sum_{\tau=1}^{3}f(\tau)g(4-\tau)
∑τ=13?f(τ)g(4?τ)。可以形象地绘制成下图：
如果稍微扩展一点，比如说我们认为 f ( 0 ) f(0) f(0) 或者 g ( 0 ) g(0) g(0) 等是可以取到的，只是它们的值为0而已。那么该公式可以写成 ∑ τ = ? ∞ ∞ f ( τ ) g ( 4 ? τ ) \sum_{\tau=-\infty}^{\infty}f(\tau)g(4-\tau) ∑τ=?∞∞?f(τ)g(4?τ)。仔细观察，这其实就是卷积 ( f ? g ) ( 4 ) (f*g)(4) (f?g)(4)。如果将它写成内积的形式，卷积其实就是 [ f ( ? ∞ ) , ? ? , f ( 1 ) , ? ? , f ( ∞ ) ] ? [ g ( ∞ ) , ? ? , g ( 3 ) , ? ? , g ( ? ∞ ) ] [f(-\infty),\cdots,f(1),\cdots,f(\infty)] \cdot [g(\infty),\cdots,g(3),\cdots,g(-\infty)] [f(?∞),?,f(1),?,
