节点的度

图论中：
节点度是指和该节点相关联的边的条数，又称关联度。
特别地，对于有向图，
节点的入度 是指进入该节点的边的条数；
节点的出度是指从该节点出发的边的条数。

入度是图论算法中重要的概念之一。它通常指有向图中某点作为图中边的终点的次数之和。

入度的常见情况：
入度为0，顾名思义，入度为0指有向图中的点不作为任何边的终点，也就是说，这一点所连接的边都把这一点作为起点。

来自原文

介数

介数通常分为边介数和节点介数两种.节点介数定义为网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例.边介数定义为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例.所以首先应求出各点到各点的最短路径，可用迪杰斯特拉算法，然后算出经过某一节点有几条路径，之后求出节点介数。一般来说，节点介数相对于边介数好算一些。 介数反映了相应的节点或者边在整个网络中的作用和影响力，是一个重要的全局几何量，具有很强的现实意义。例如，在社会关系网或技术网络中，介数的分布特征反映了不同人员、资源和技术在相应生产关系中的地位，这对于发现和保护关键资源、技术和人才具有重要意义。

来自原文

度与介数

衡量网络节点重要性的指标有很多，但每一个指标的侧重点不一样。度表征的网络节点重要性着重点在于该节点邻居节点的多少，我们认为邻居节点越多那么节点在网络中的重要性越强。该指标的优势在于计算非常简单，但劣势也相当明显，正如 @lyojo 提到的，节点的重要性也与邻居节点的重要性有很大关系，这是度不能体现的。另外再举一个极端的例子，比如一个网络有两个团体，每个团体都很大，但是只有一个节点A是作为两个团体的桥梁，即A既与团体一中的某个节点B相连，又与团体二中的某个节点C相连，但A只有AB两个邻居，很显然C的度为2。我们假设B与团体一中另外99个节点相连，那么B的度为100。以度来看的话B远重要于A，但是很明显如果团体一与团体二之间的人想要联系，A是避不开的，那么一旦A这个节点被移除了，团体一和团体二就孤立了。相反移除B就没有这么大的危害。那么有什么可以描述这种重要性呢？这就是介数了。介数更多的是去表征节点在连通网络中起到的作用，其本身的定义就是最短路径经过节点的次数来的。但它的劣势也很明显，计算起来很复杂。要是对网络节点重要性有兴趣的话可以看下吕琳媛教授的论文Vital nodes identification in complex networks。

来自原文

小世界网络 small-world network

小世界网络是一种数学图。在此类图中，绝大多数节点彼此之间并不相邻，但任一给定节点的邻居们却很可能彼此是邻居，并且大多数节点都可以从任意其他节点，用较少的步或跳跃访问到。具体来说，小世界网络的定义如下：如果网络中随机选择的两个节点之间的距离L（即访问彼此所需要的步数），与网络中节点数量N的对数成比例增长，（即$L\propto \log N$），且网络的集聚系数 Clustering Coefficient不小，那么，这样的网络就是小世界网络。在社交网络中，这种网络属性意味着一些彼此并不相识的人，可以通过一条很短的熟人链条被联系在一起，这也就是小世界现象。许多经验网络图都展示出了小世界现象，例如社交网络、互联网的底层架构、诸如Wikipedia的百科类网站以及基因网络等等。

1998年，Duncan J. Watts和Steven Strogatz提出，小世界网络是一类随机图[2]。他们指出，这类网络图可以通过两个独立的结构特征，即集聚系数和平均节点间距离（也称作平均最短路径长度）来进行识别。根据ER随机图模型构造的纯随机图，会展现出较小的最短路径长度（通常随着节点数对数值的变化而变化）以及较小的集聚系数。Watts和Strogatz验证了这一点，事实上，现实世界中很多网络的平均最短路径长度都较短，而集聚系数又远高于普通随机图。Watts和Strogatz随后提出了一种新的图模型（即现在的Watts-Strogatz模型），该模型具备两个特征：(1)平均最短路径长度较小，(2)集聚系数较大。

来自集智百科

在网络理论中，小世界网络是一类特殊的复杂网络结构，在这种网络中大部份的节点彼此并不相连，但绝大部份节点之间经过少数几步就可到达。

在日常生活中，有时你会发现，某些你觉得与你隔得很“遥远”的人，其实与你“很近”。小世界网络就是对这种现象（也称为小世界现象）的数学描述。用数学中图论的语言来说，小世界网络就是一个由大量顶点构成的图，其中任意两点之间的平均路径长度比顶点数量小得多。除了社会人际网络以外，小世界网络的例子在生物学、物理学、计算机科学等领域也有出现。许多经验中的图可以由小世界网络来作为模型。万维网、公路交通网、脑神经网络和基因网络都呈现小世界网络的特征。

来自王伟华

六度分隔理论

六度分隔（Six Degrees of Separation）理论。简单地说：“你和任何一个陌生人之间所间隔的人不会超五个，也就是说，最多通过六个人你就能够认识任何一个陌生人。

“六度分隔”说明了社会中普遍存在的“弱纽带”，但是却发挥着非常强大的作用。有很多人在找工作时会体会到这种弱纽带的效果。 通过弱纽带人与人之间的距离变得非常“相近”。

数学解释：若每个人平均认识260人，其六度就是260的6次方=308，915，776，000，000（约300万亿）。消除一些节点重复，那也几乎覆盖了整个地球人口若干多倍。

来自百度百科

无标度网络 scale-free network

无标度网络具有严重的异质性，其各节点之间的连接状况（度数）具有严重的不均匀分布性：网络中少数称之为Hub点的节点拥有极其多的连接，而大多数节点只有很少量的连接。少数Hub点对无标度网络的运行起着主导的作用。从广义上说，无标度网络的无标度性是描述大量复杂系统整体上严重不均匀分布的一种内在性质。

scale - free network, 现实世界的网络大部分都不是随机网络，少数的节点往往拥有大量的连接，而大部分节点却很少，一般而言他们符合zipf定律，(也就是80/20马太定律)。将度分布符合幂律分布的复杂网络称为无标度网络。

来自原文

随机网络：没有中心节点，大部分节点都均匀的连在一起。

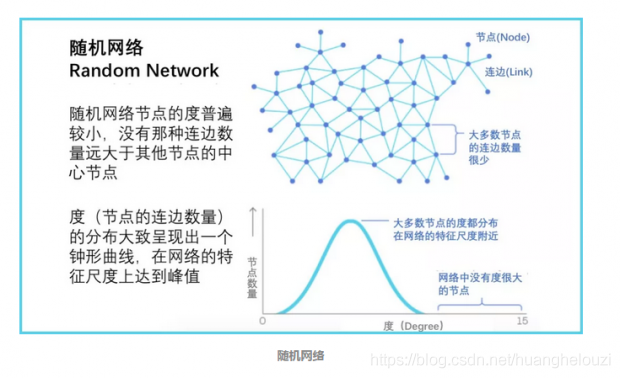
scale-free network：大部分的连接都集中在少数的中心

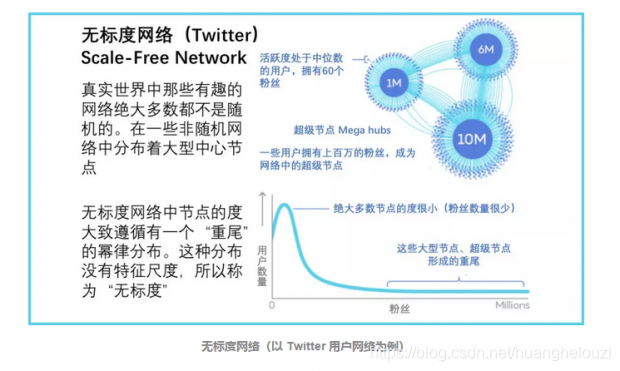
来自原文

齐普夫定律

Zipf定律一般指齐普夫定律.

它可以表述为：如果把一篇较长文章中每个词出现的频次统计起来，按照高频词在前、低频词在后的递减顺序排列，并用自然数给这些词编上等级序号，即频次最高的词等级为1，频次次之的等级为2，……，频次最小的词等级为$D$。若用$f$表示频次，$r$表示等级序号，则有$f?r=C$(C为常数)，方程式表示词使用的总次数和词频表上的位置之间有一个固定比率。人们称该式为齐普夫定律。

来自原文

幂律分布

节点具有的连线数和这样的节点数目乘积是一个定值，也就是几何平均是定值，比如有10000个连线的大节点有10个，有1000个连线的中节点有100个，100个连线的小节点有1000个，在对数坐标上画出来会得到一条斜向下的直线。

也就是： $定值=连线数?节点数$

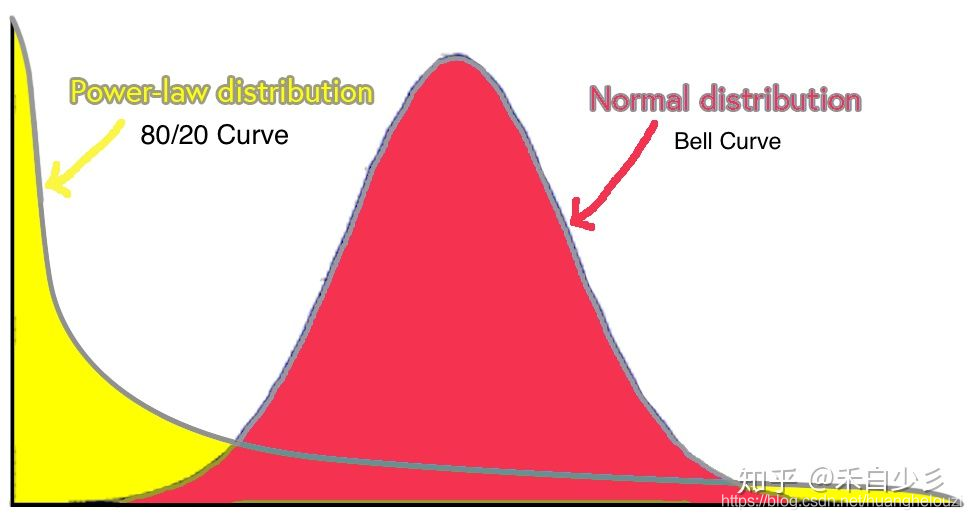
幂律分布表现为一条斜率为幂指数的负数的直线,这一线性关系是判断给定的实例中随机变量是否满足幂律的依据。

来自原文

平均路径长度

平均路径长度也称为特征路径长度或平均最短路径长度，指的是一个网络中两点之间最短路径长度（或称距离）的平均值。从一个节点$s_i$出发，经过与它相连的节点，逐步“走”到另一个节点$s_j$所经过的路途，称为两点间的路径。其中最短的路径也称为两点间的距离，记作$\mathrm{dist}(i,j)$。而平均路径长度定义为：

${\mathrm{dist}}_c=\frac{2}{N(N+1)}\sum _{i?N}\sum _{j?i}\mathrm{dist}(i,j)$
这其中$N$是节点数目，并定义节点到自身的最短路径长度为0。如果不计算到自身的距离，那么平均路径长度的定义就变成：

${\mathrm{dist}}_c=\frac{2}{N(N?1)}\sum _{i?N}\sum _{j>i}\mathrm{dist}(i,j)$

来自赏月斋

集聚系数 Clustering Coefficient

集聚系数（也称群聚系数、集群系数）是用来描述图或网络中的顶点（节点）之间结集成团的程度的系数。具体来说，是一个点的邻接点之间相互连接的程度。例如在社交网络中，你的朋友之间相互认识的程度。一个节点$s_i$的集聚系数 $C(i)$等于所有与它相连的顶点相互之间所连的边的数量，除以这些顶点之间可以连出的最大边数。显然 $C(i)$ 是一个介于0与1之间的数。 C ( i ) {\displaystyle C(i)}