在机器学习领域，概率分布对于数据的认识有着非常重要的作用。不管是有效数据还是噪声数据，如果知道了数据的分布，那么在数据建模过程中会得到很大的启示。

首先，如下图所示8个特征数据概率分布情况（已经做归一化），这些特征是正态分布、伯努利分布，还是泊松分布、幂律分布？

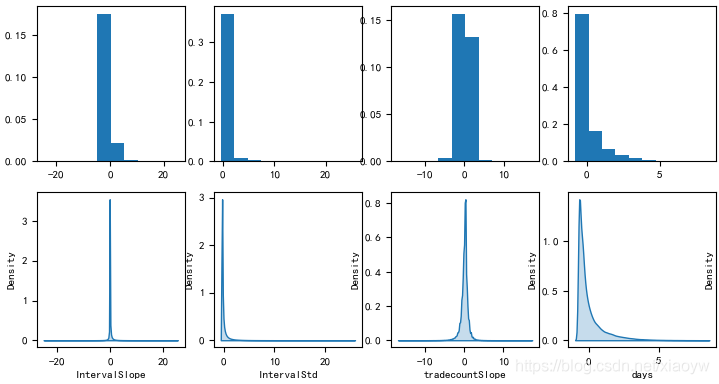
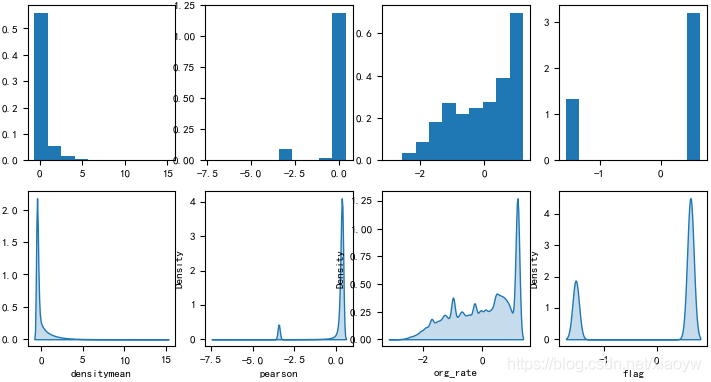
在高斯法则生效的领域，平均值可以代表整体。但是在幂律法则统治的领域，平均值毫无意义。高斯法则和幂律法则的典型代表是分别身高和财富，把姚明放到100个人中，并不会显著改变平均身高，但把比尔·盖茨放到100个人中，就会极大改变平均财富。

在高斯法则生效的领域，所有人跟平均值的差距不会很大；但是在幂律法则分布的领域，跟平均值的差距就会大到惊人。

正态法则和幂律法则，细思极恐。带着问题，我们开始概率分布之旅。

1. 概率分布概述

概率分布，是指用于表述随机变量取值的概率规律。将随机变量作为横轴，概率作为纵轴，把随机变量与对应变量画上去，构成一个图形，这个图像就是概率分布的直观表示。通常也用概率分布函数表示$F(x)$来描述一个概率分布，概率分布函数被定义为：
F ( x ) = P { X < x } F ( x ) =P\{X<x\} F(x)=P{X<x}

总之概率分布也可以理解为一个函数，它刻画了随机变量与概率的映射关系，给定一个概率分布，就可以求任何随机变量对应的概率了。当一个随机变量与它的概率满足某一个概率分布的映射关系时，则称这个随机变量服从该概率分布。

如下图为常用概率分别关系图。

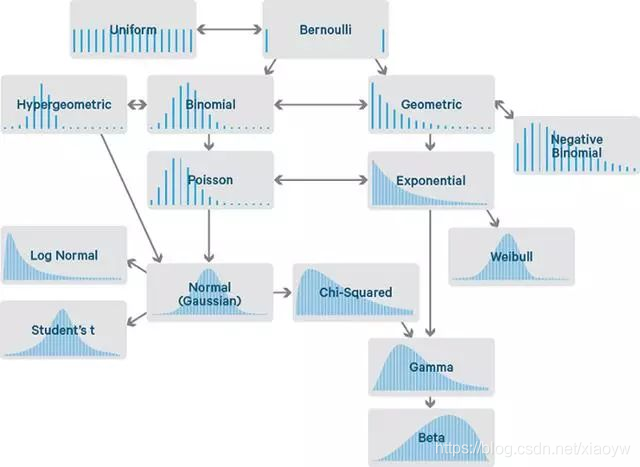
2. 常用概率分布

2.1. 均匀分布

均匀分布在 [a，b] 上具有相同的概率值，是简单概率分布。
均匀分布可以很容易地从伯努利分布中得出。在这种情况下，结果的数量可能不受限制，并且所有事件的发生概率均相同。例如掷骰子，存在多个可能的事件，每个事件都有相同的发生概率。

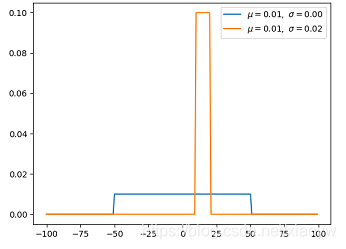
2.2. 伯努利分布

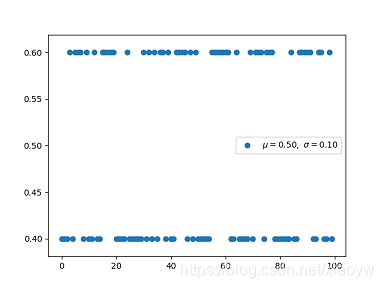
伯努利分布（Bernoulli Distribution）是单个二值随机变量的分布，是一种离散分布，又称为 “0-1 分布” 或 “两点分布”。例如抛硬币的正面或反面，物品有缺陷或没缺陷，病人康复或未康复，此类满足「只有两种可能，试验结果相互独立且对立」的随机变量通常称为伯努利随机变量。

假设二值其中之一的概率等于$p$，而对于互斥对立面面则是$（1?p）$（包含所有可能结果的互斥事件的概率总和为1）。

对于伯努利分布来说，其离散型随机变量期望为：
$E(x)=\sum x\times p(x)=1\times p+0\times (1?p)=p$
$E(x^2)=\sum x\times p(x^2)=1^2\times p+0^2\times (1?p)=p$

方差为：
$Var(x)=E(x^2)?(E(x){)}^2=p?p^2=p(1?p)$

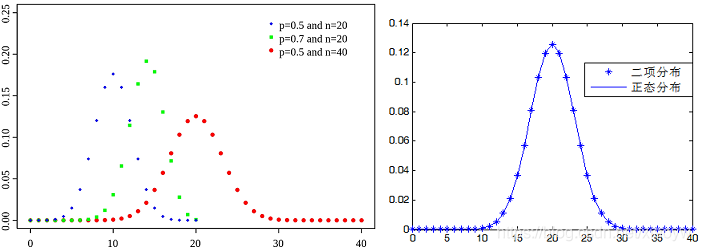
2.3. 二项分布

二项分布（binomial distrubution）就是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果，而且两种结果发生与否互相对立，并且相互独立，与其它各次试验结果无关，事件发生与否的概率在每一次独立试验中都保持不变，则这一系列试验总称为n重伯努利实验，当试验次数为1时，二项分布服从0-1分布。

P { X = k } = ( n k ) p k ( 1 ? p ) ( n ? k ) P\{X=k\}=\binom{n}{k}p^k(1-p)^{(n-k)} P{X=k}=(kn?)pk(1?p)(n?k)

式中$k=0,1,2,...,n$，$\left(\genfrac{}{}{0ex}{}{n}{k}\right)=\frac{n!}{k!(n?k)!}$是二项式系数，又记为$C_n^k$。

二项式分布的主要特征是：

给定多个试验，每个试验彼此独立（一项试验的结果不会影响另一项试验）。

每个试验只能得出两个可能的结果（例如，获胜或失败），其概率分别为p和（1- p）。

如果获得成功概率（p）和试验次数（n），则可以使用以下公式计算这n次试验中的成功概率（x）。