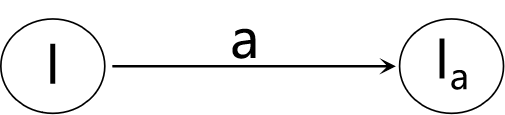NFA、DFA之间的转化
NFA的等价转化
假定有如下图所示的非确定状态机(NFA) M = <S, ∑, δ, S0, F>
| 符号 | 含义 |
|---|
| S | 状态集合 |
| ∑ | 字母表 |
| δ | 转换关系 |
| S0 | 初始状态集 |
| F | 终止状态集 |

我们对M的状态转换图进行以下改造:
- 引进新的初态结点X和终态结点Y,X,Y?S,从X到S0中任意状态结点连一条ε箭弧, 从F中任意状态结点连一条ε箭弧到Y
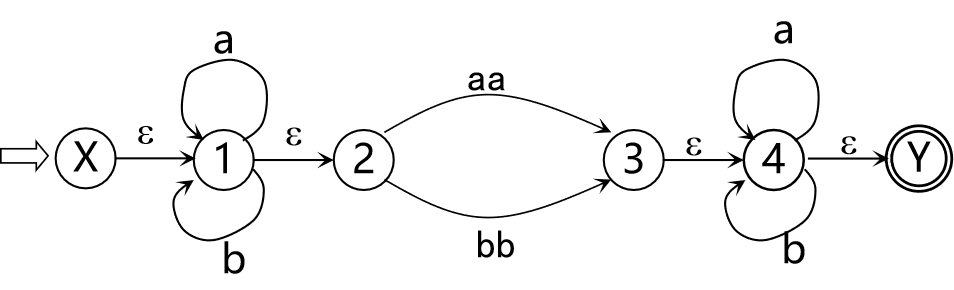
这样,我们就能确保初态和终态的唯一性。 - 对M的状态转换图进一步施行替换,通过新引入的状态k,将弧上的标记全部替换为单个字符,例如:

由此,M被替换为:
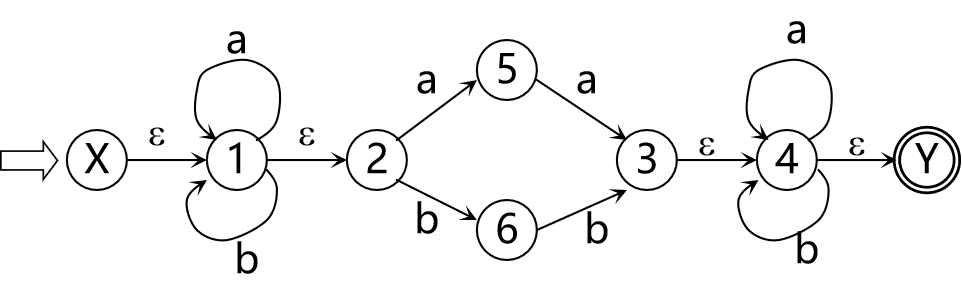
如果每条弧只标记为∑上的一个字符或ε,我们就把这个NFA记为M’ 。
显然 L(M’)=L(M)
NFA确定化——子集法
目的:解决ε弧和转换关系
- 设I是的状态集的一个子集,定义I的ε-闭包ε-closure(I)为:
- 若s∈I,则s∈ε-closure(I);
- 若s∈I,则从s出发经过任意条ε弧而能到达的任何状态s’都属于ε-closure(I)
- 设a是∑中的一个字符,定义 Ia= ε-closure(J) 。其中,J为I中的某个状态出发经过一条a弧而到达的状态集合:
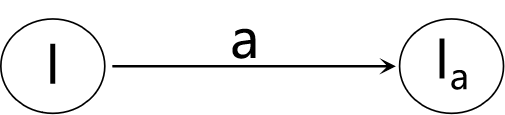
例:对于如下NFA,假定 I = ε-closure({1}),求出I和Ia
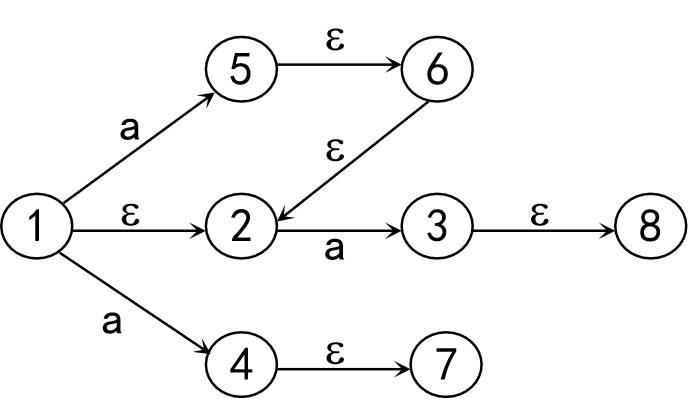
解:I = ε-closure({1}) = {1,2}
假定J为I中的某个状态出发经过一条a弧而到达的状态集合,那么 J = {5,4,3}。其中,状态1经过a弧到达状态5,4,状态2经过a弧到达状态3。
于是,Ia = ε-closure(J) = ε-closure({5,4,3}) = {5,6,2,4,7,3,8}。
闭包传递关系如下:
<ε-closure id="J">
<state id="5">
<state id="6">
<state id="2"/>
</state>
</state>
<state id="4">
<state id="7"/>
</state>
<state id="3">
<state id="8"/>
</state>
</ε-closure>
操作步骤
DFA与NFA的等价性证明
- 把表看成状态转换矩阵,子集视为状态
- 转换表唯一刻划了一个确定的有限自动机M
- 初态是ε-closure({X})
- 终态是含有原终态Y的子集
- 不难看出,这个DFA M与M’等价
- 对于每个NFA M存在一个DFA M ’ ,使得 L(M)=L(M’)
显然,NFA和DFA等价
DFA的化简
目标:对于给定的DFA M,寻找一个状态数比M少的DFA M’,使得L(M)=L(M’)
状态的等价性
- 假设s和t为M的两个状态,称s和t 等价:
如果从状态s出发能读出某个字α而停止于终态,那么同样,从t出发 也能读出 α而停止于终态;反之亦然 - s和t 不等价:
存在一个字α,要么s读出α停止于终态而t读出α停止于非终态,要么t读出α停止于终态而s读出α停止于非终态
此时,称它们是 可区别的
化简的基本思想
把M的状态集划分为一些不相交的子集,使得任何两个不同子集的状态是可区别的,而同一子集的任何两个状态是等价的。
最后,让每个子集选出一个代表,同时消去其他状态。
例:按照上述原则对DFA的状态集合S进行第一次划分,正确的分法是将S分为终态和非终态
说明:终态读出ε后依然停留在终态,非终态读出ε后依然在非终态。
化简步骤
- 首先,把S划分为终态和非终态两个子集,形成基本划分π。
- 假定到某个时候,现行划分π已含m个子集,记为π={I(1),I(2),…,I(m)},检查π中的每个子集看是否能进一步划分:
- 对某个I(i),令I(i)={s1,s2, …,sk},若存在一个输入字符a使得Ia(i) 不会包含在π的某个子集I(j)中,则至少应把I(i)分为两个部分。
- 假定状态s1和s2是I(i)={s1,s2, …,sk}中的两个状态,它们经a弧分别到达t1和t2,而t1和t2属于π中的两个不同子集
- 说明有一个字α, t1读出α后到达终态,而t2读出α后不能到达终态,或者反之
- 那么对于字aα , s1读出aα后到达终态,而s2读出aα不能到达终态,或者反之
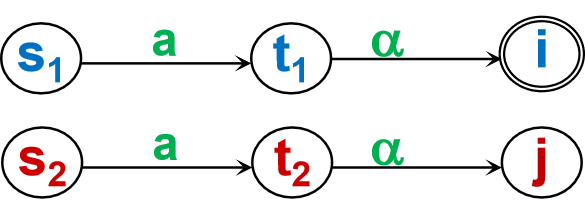
- 所以s1和s2不等价,应当进行划分
- 将I(i)分成两半,一半含有s1,一半含有s2
- I(i1)含有s1: I(i1) ={s|s∈I(i)且s经a弧到达t, 且t与t1属于π中的同一子集}
- I(i2)含有s2: I(i2)=I(i) - I(i1)
- 一般地,对某个a和I(i),若Ia(i) 落入π中 N个不同子集,则应把I(i)划分成N个不相交的组,使得每个组J的Ja都落入π的同一子集。
- 重复上述过程,直到π所含子集数不再增长(所有子集都无法再划分)
- 对于上述最后划分π中的每个子集,我们选取每个子集I中的一个状态代表其他状态,则可得到化简后的DFA M’
- 若I含有原来的初态,则其代表为新的初态(唯一),若I含有原来的终态,则其代表为新的终态(不唯一)
实例
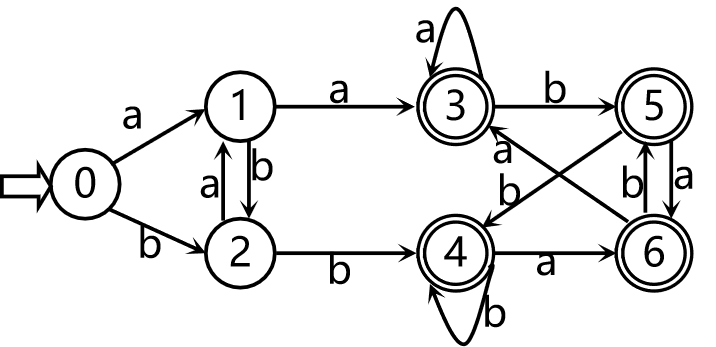
对于上图是我们从NFA转换得到的DFA,我们对其状态做出化简:
- 用ε区分终态和非终态,得到
I(1)={0, 1, 2} , I(2)={3, 4, 5, 6}
现行划分π={I(1), I(2)} - I(1)识别a之后形成能到达{1,3},因此 I(1)a={1,3}
由于I(1)a的元素同时位于现行划分π两个子集I(1)和I(2)中,我们要对I(1)进行划分,注意到0,2识别a之后都到达1,因此要将{0,2}分为一组,剩下的{1}放到另一组,即:I(11)={0,2} , I(12)={1}
现行划分π={I(11),I(12), I(2)} - 注意到 I(11)b={2,4},2在I(11)中,4在I(2)中,其中0识别b之后转为2,2识别b后转为4。因此要将{0}分为一组,剩下的{2}放到另一组,即:I(111)={0}, I(112)={2}
现行划分π={I(111),I(112),I(12), I(2)} - 由于I(2)a={3,6}的元素都在I(2)中,I(2)b={4,5}的元素都在现行划分的同一个子集(I(2))中,因此 没有子集可以继续划分了。
现行划分π={I(111),I(112),I(12), I(2)}
即π={{0},{1},{2},{3,4,5,6}},同一子集内的状态都是等价的,不同子集的状态都是可区别的。 - 用状态3代表{3,4,5,6},即所有从{4,5,6}射出的弧都由{3}射出,所有射入{4,5,6}的弧都射入到{3},化简后的效果如下:
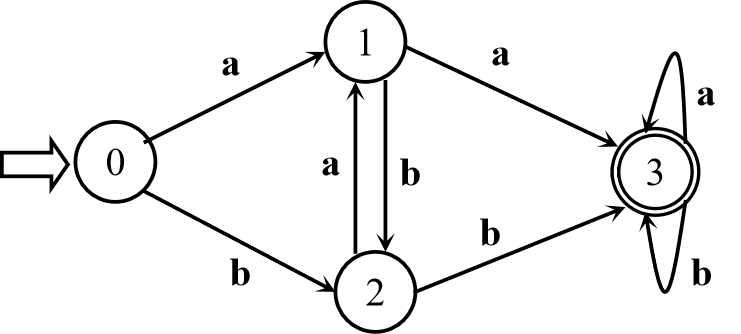
可见状态数大大减少。
补充:根据上例的操作,我们可以通过列表大大简化化简步骤,如图:
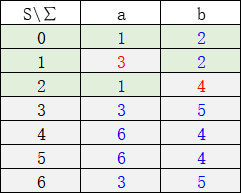
蓝色字表示现行划分内的一个状态机识别某个字符后仍在这个划分内,红色字代表跳出了这个划分,具体跳入了哪个划分可以根据底色确定(这两个都跳入了灰色的划分)
检查状态机所在行的跳入情况,只有底色完全一致(考虑顺序)的({0}、{1}、{2}、{3,4,5,6})才属于同一个新的现行划分,并据此重新给不同状态机上色。
如果重新上色后同一划分内底色仍然一致,结束,否则继续划分,并再次上色。
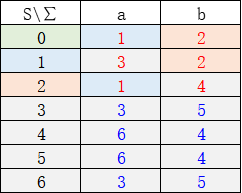
(新划分内每一划分底色一致)
最后,根据底色的分布情况可以重新画出简化的DFA
小结
请点击小标题观看视频
cs