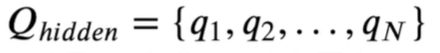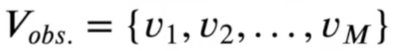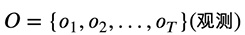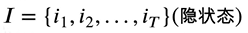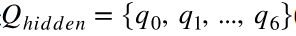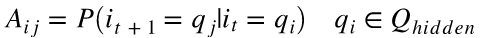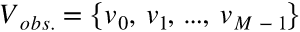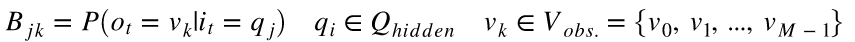注:
一元语法模型:
我考上大学只与考试当天的我有关,与前一天模拟考的我没有半毛钱关系
二元语法模型:
我考上大学与我前一天模拟考的我有关
书接上回
我们先做一些约定:
Qhidden为所有隐藏状态种类的合集,有N种
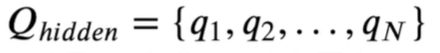
例如我们之前定义了七个标签(https://www.cnblogs.com/DAYceng/p/14923065.html),那么N = 7
Vobs表示可观测的序列的合集(这里由汉字组成)
其中,V为单个的字,M为已知字的个数
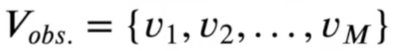
有一串自然语言文本O,共T个字,则观测合集可表示为
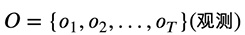
而观测到的实体对应的实体标记就是隐状态合集I
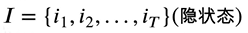
I与O一一对应并且长度一致
注:常称T为时刻,如上式中共有T个时刻(T个字)
HMM的假设
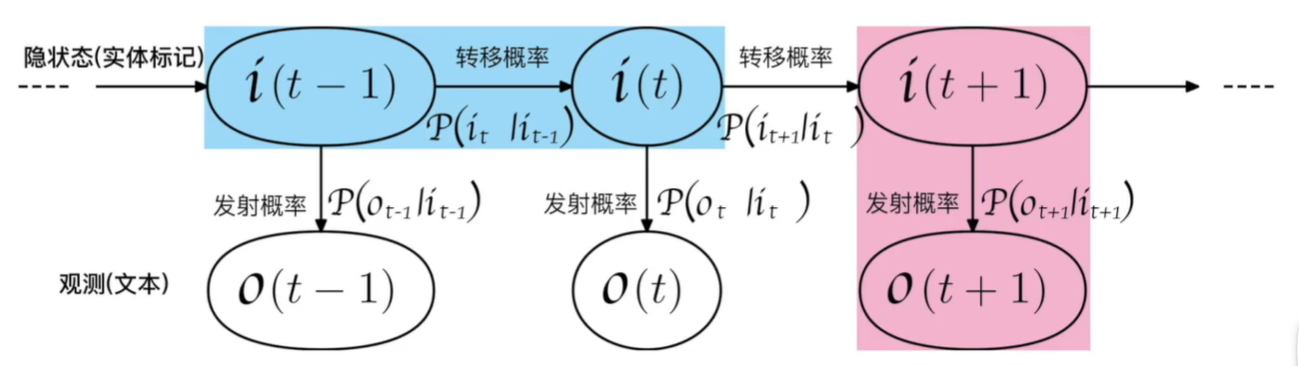
图片出处:https://github.com/aespresso/a_journey_into_math_of_ml
假设一:
当前第 个隐状态(实体标签)只跟前一时刻的
个隐状态(实体标签)只跟前一时刻的 隐状态(实体标签)有关,连续多个状态构成隐马尔可夫链I(隐状态合集),与除此之外的其他隐状态无关。
隐状态(实体标签)有关,连续多个状态构成隐马尔可夫链I(隐状态合集),与除此之外的其他隐状态无关。
例如,上图中:蓝色的部分指的是 只与
只与 有关,而与蓝色区域之外的所有内容都无关,而
有关,而与蓝色区域之外的所有内容都无关,而 指的是隐状态
指的是隐状态 从
从 时刻转向t时刻的概率。
时刻转向t时刻的概率。
假设二:
观测独立的假设,我们上面说过,HMM模型中是由隐状态序列(实体标记)生成可观测状态(可读文本)的过程,观测独立假设是指在任意时刻观测 只依赖于当前时刻的隐状态i,与其他时刻的隐状态无关。
只依赖于当前时刻的隐状态i,与其他时刻的隐状态无关。
例如上图中:粉红色的部分指的是 只与
只与 有关,跟粉红色区域之外的所有内容都无关。
有关,跟粉红色区域之外的所有内容都无关。
至此,我们确定了状态与观测之间的关系。
接下来将介绍HMM用于模拟时序序列生成过程的三个要素(即HMM模型的三个参数):
初始状态概率向量
初始隐状态概率通常用π表示(不是圆周率!!)

该表达式的含义:
自然语言序列的第一个字 的实体标签是
的实体标签是 的概率,即初始隐状态概率
的概率,即初始隐状态概率
而初始状态可表示如下:p(y1丨π),给定π,初始状态y1的取值分布就确定了
状态转移概率矩阵
初始状态确定之后,如何转移到初始状态的下一个状态呢?
还记得马尔可夫假设第一条吗?t+1时刻的状态只取决于t时刻状态
我们上面提到了 指的是隐状态
指的是隐状态 从
从 时刻转向
时刻转向 时刻的概率
时刻的概率
比如说我们现在实体标签一共有 种, 也就是
种, 也就是 (注意
(注意 是所有可能的实体标签种类的集合), 也就是
是所有可能的实体标签种类的集合), 也就是
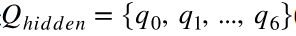
(注意我们实体标签编号从 算起)。
算起)。
假设在 时刻任何一种实体标签都可以在
时刻任何一种实体标签都可以在 时刻转换为任何一种其他类型的实体标签
时刻转换为任何一种其他类型的实体标签
由排列组合不难得出以下结论:总共可能的转换的路径有 种, 所以我们可以做一个
种, 所以我们可以做一个 的矩阵来表示所有可能的隐状态转移概率.
的矩阵来表示所有可能的隐状态转移概率.

图片出处:https://github.com/aespresso/a_journey_into_math_of_ml
如图所示即为状态转移概率矩阵,设矩阵为 矩阵, 则
矩阵, 则 表示矩阵中第i行第j列:
表示矩阵中第i行第j列:
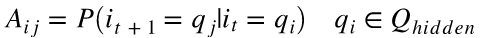
该表达式的含义:
某时刻实体具有一个标签,而下一时刻该标签转换到某标签的概率,即 时刻实体标签为
时刻实体标签为 , 而在
, 而在 时刻实体标签转换到
时刻实体标签转换到 的概率
的概率
发射概率矩阵
回到最初的问题,有了(隐)状态yt之后,如何确定观测xt的概率分布呢?
根据尔可夫假设第二条,任意时刻观测 只依赖于当前时刻的隐状态
只依赖于当前时刻的隐状态 , 也叫做发射概率,描述了隐状态生成观测结果的过程
, 也叫做发射概率,描述了隐状态生成观测结果的过程
设我们的字典里有 个字,
个字,
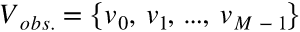
(注意这里下标从0算起, 所以最后的下标是 , 一共有
, 一共有 种观测), 则每种实体标签(隐状态)可以生成
种观测), 则每种实体标签(隐状态)可以生成 种不同的汉字(也就是观测), 这一过程可以用一个发射概率矩阵来表示, 它的维度是
种不同的汉字(也就是观测), 这一过程可以用一个发射概率矩阵来表示, 它的维度是
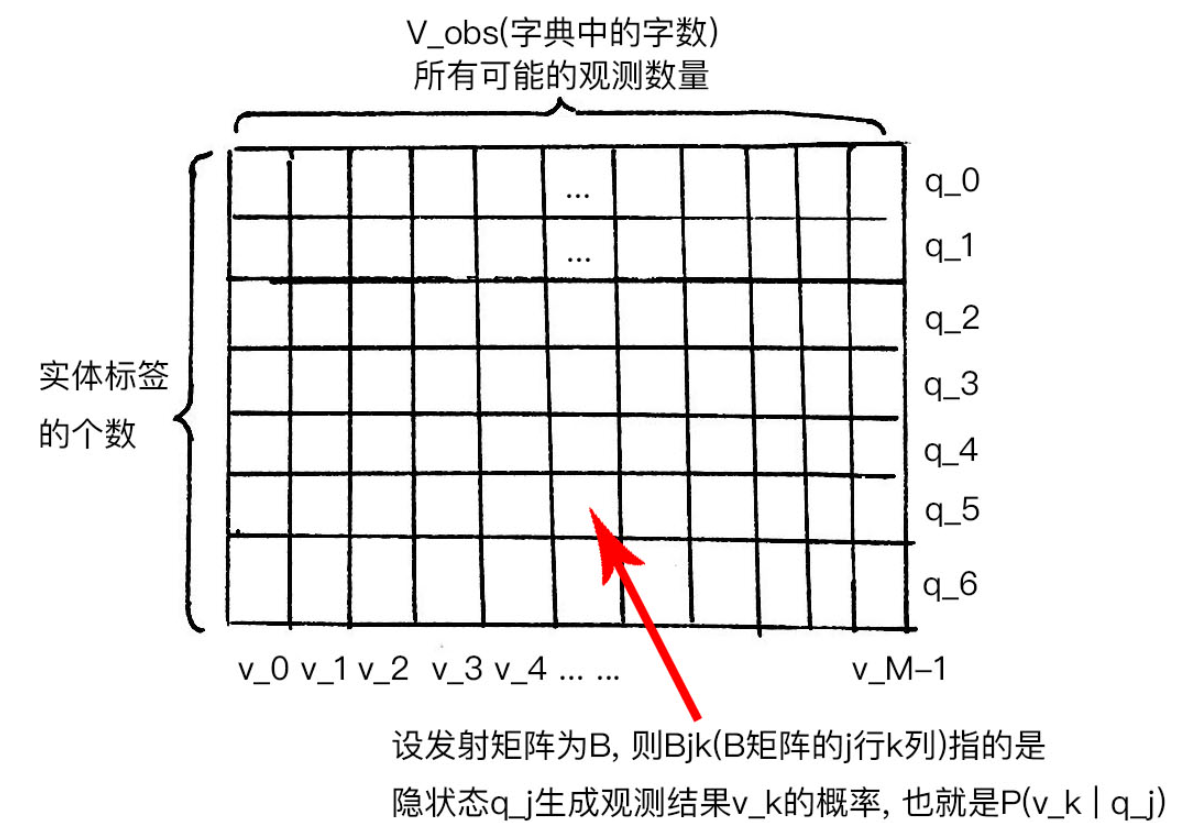
图片出处:https://github.com/aespresso/a_journey_into_math_of_ml
设这个矩阵为 矩阵, 则
矩阵, 则 表示矩阵中第
表示矩阵中第 行第
行第 列:
列:
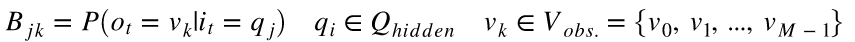
该表达式的含义:
在 时刻由实体标签(隐状态)
时刻由实体标签(隐状态) 生成汉字(观测结果)
生成汉字(观测结果) 的概率.
的概率.
至此,HMM的概念部分基本介绍完毕