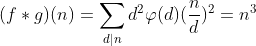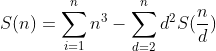https://www.luogu.org/problem/P3768
题意很简单就是求这个:
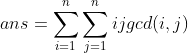
为了方便我们用(i,j)表示gcd(i,j),然后开始快乐的推公式吧:
![ans=\sum_{d=1}^{n}d\sum_{i=1}^{n}\sum_{j=1}^{n}ij[(i,j)=d]=\sum_{d=1}^{n}d^{3}\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{n}{d} \right \rfloor}ij[(i,j)=1]](http://style.iis7.com/uploads/2021/09/14482973575.gif)
看见后面那一坨直接莫比乌斯反演:
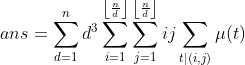
然后根据套路枚举t:
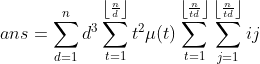
后面一部分就是等差数列通项公式,所以后面就是变形为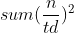
然后再根据套路令T=td,枚举T:
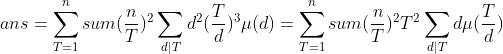
我们观察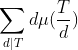 这部分刚好是狄利克雷卷积的标准形式
这部分刚好是狄利克雷卷积的标准形式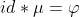
因此这部分就是欧拉函数。所以最终公式:
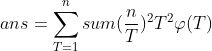
其实这都是吃饱了的做法,如果不直接无脑用莫比乌斯反演而是用这个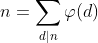 ,在题目上的那个式子中吧gcd给替换了看看呢:
,在题目上的那个式子中吧gcd给替换了看看呢:
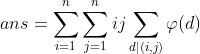
然后枚举d:
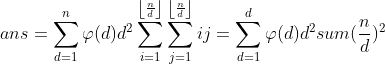
是不是这样要简单很多呢,我们暂且称为欧拉反演吧。
观察上面的式子前面可以分块做,那就要求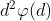 的前缀和了,那当然就是杜教筛了。
的前缀和了,那当然就是杜教筛了。
我们卷积平方就可以了: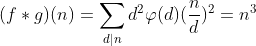
所以杜教筛就可以这样筛了: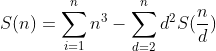
其他就没什么了。
#include "bits/stdc++.h"
using namespace std;
const int N = 5000000 + 10;
typedef long long ll;
int vis[N], cnt = 0;
ll pri[N], phi[N], p, sum_f[N], inv6, inv2, n;
ll quick(ll a, ll n, ll p) {
ll ans = 1;
while (n) {
if (n & 1) ans = ans * a % p;
a = a * a % p;
n >>= 1;
}
return ans;
}
void init() {
phi[1] = vis[1] = 1;
for (int i = 2; i < N; i++) {
if (!vis[i]) {
pri[++cnt] = i;
phi[i] = i - 1;
}
for (int j = 1; j <= cnt && i * pri[j] < N; j++) {
vis[i * pri[j]] = 1;
if (i % pri[j] == 0) {
phi[i * pri[j]] = phi[i] * pri[j] % p;
break;
}
phi[i * pri[j]] = phi[i] * phi[pri[j]];
}
}
for (int i = 1; i < N; i++) {
sum_f[i] = (sum_f[i - 1] + 1LL * i * i % p * phi[i] % p) % p;
}
}
unordered_map <ll, ll> mp;
ll get3(ll x) {
x %= p;
ll tmp = x * (x + 1) % p * inv2 % p;
return tmp * tmp % p;
}
ll get2(ll x) {
x %= p;
ll ret = x * (x + 1) % p * (2 * x % p + 1) % p * inv6 % p;
return ret;
}
ll pre_f(ll x) {
if (x < N) return sum_f[x];
if (mp.count(x)) return mp[x];
ll ans = 0;
for (ll l = 2, r; l <= x; l = r + 1) {
r = x / (x / l);
ans = (ans + (get2(r) - get2(l - 1)) % p * pre_f(x / l) % p);
if (ans < 0) ans += p;
}
ans = (get3(x) - ans) % p;
if (ans < 0) ans += p;
return mp[x] = ans;
}
ll solve(ll x) {
ll ans = 0;
for (ll l = 1, r; l <= x; l = r + 1) {
r = x / (x / l);
ll t = get3(x / l);
ans = (ans + t * (pre_f(r) - pre_f(l - 1)) % p) % p;
if (ans < 0) ans += p;
}
return ans;
}
int main() {
scanf("%lld%lld", &p, &n);
inv2 = quick(2, p - 2, p);
inv6 = quick(6, p - 2, p);
init();
///ll ans = 0;
///for (ll i = 1; i <= n; i++) {
/// ans += get3(n / i) * i % p * i % p * phi[i] % p;
/// ans %= p;
///}
///cout << ans << endl;
printf("%lld\n", solve(n));
return 0;
}
?
cs

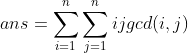
![ans=\sum_{d=1}^{n}d\sum_{i=1}^{n}\sum_{j=1}^{n}ij[(i,j)=d]=\sum_{d=1}^{n}d^{3}\sum_{i=1}^{\left \lfloor \frac{n}{d} \right \rfloor}\sum_{j=1}^{\left \lfloor \frac{n}{d} \right \rfloor}ij[(i,j)=1]](http://style.iis7.com/uploads/2021/09/14482973575.gif)
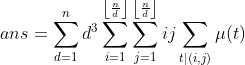
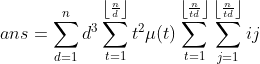
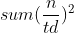
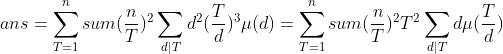
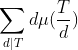 这部分刚好是狄利克雷卷积的标准形式
这部分刚好是狄利克雷卷积的标准形式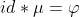
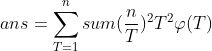
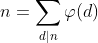 ,在题目上的那个式子中吧gcd给替换了看看呢:
,在题目上的那个式子中吧gcd给替换了看看呢: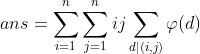
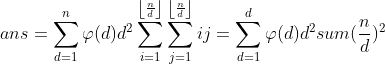
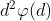 的前缀和了,那当然就是杜教筛了。
的前缀和了,那当然就是杜教筛了。