初见安~又是好久没写博客了……加上CSP才炸了一波。
目录
一、整除分块
题解
二、积性函数
三、狄利克雷卷积
四、欧拉函数
五、莫比乌斯函数(mu)
六、莫比乌斯反演
一、整除分块
看个例题:洛谷P2261 余数求和

题解
对于取模操作,考虑换成整除:
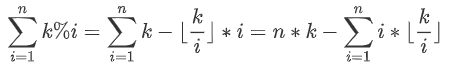
后面就显然是一个整除分块了。
考虑k/i,显然可以有一段区间l~r满足k整除他们的值相同。如果我们O1跳这些区间的话均摊复杂度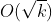 。
。
现在看该怎么跳这些区间。
假设当前区间最左端为i,有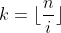 。则:
。则:

所以区间为[i,i']。
回到这个题,每一项乘的系数加起来就是等差数列求和,直接求和即可。
上代码——
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<queue>
#define int long long
using namespace std;
typedef long long ll;
int read() {
int x = 0, f = 1, ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
return x * f;
}
int n, k;
signed main() {
n = read(), k = read();
long long ans = 0;
for(int i = 1, j; i <= min(n, k); i = j + 1) {//i是左端点
j = k / (k / i); if(j > n) j = n;//j是右端点
ans += (k / i) * (j - i + 1) * (i + j) / 2;//k/i乘上系数的等差数列求和
}
printf("%lld\n", 1ll * n * k - ans);
return 0;
}
好了假设你们已经会了。
多个数的整除分块的话,右端点就是所有的数整除(该数整除左端点的值)的值取min即可,也就是最前面的一个保证区间内数相同的右边界。
二、积性函数
若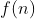 为积性函数,则满足:
为积性函数,则满足:
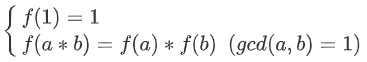
若a和b不互质也满足乘积的函数为函数的乘积的性质,则为完全积性函数。
常见的积性函数有:

以及完全积性函数:

对没错这一部分part基本上是参考的翁小泽大佬的,算是简单科普。
三、狄利克雷卷积
其实就是一种关于约数的卷积。
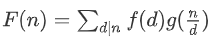
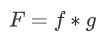
F(n)就是这两个函数的狄利克雷卷积。满足交换律、结合律和分配律。
这两个知识后面会用于证明一些东西。
四、欧拉函数
啊我知道你们都会这个。欧拉函数表示求n以内与之互质的数的个数。
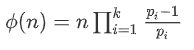
这是一个积性函数。即满足:
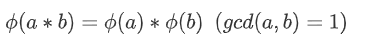
在这个性质下,因为phi是个关于质因数的函数,所以可以在线筛质数的时候把phi求出来。
但如果ab不互质呢?考虑影响因素为a和b的gcd的质因数,所以可以除以phi(gcd);又因为phi的定义式下是乘了一个gcd后再是关于质因数的累乘,所以要再乘回去一个gcd。
通式就是:
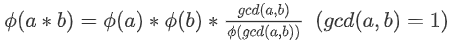
有了这个就可以线筛求phi了:
phi[1] = 1;
for(int i = 2; i <= mx; i++) {
if(!in[i]) pri[++tot] = i, phi[i] = i - 1;//质数内必然所有数与之互质。
for(int j = 1; j <= tot && i * pri[j] <= mx; j++) {
register ll g = i * pri[j];
in[g] = true, phi[g] = phi[i] * phi[pri[j]];//积性函数
if(i % pri[j] == 0) {phi[g] = phi[i] * pri[j]; break;}//通式化简可得。
}
}
欧拉函数还有一个很有用的性质是:
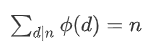
我也不会证。后面会用到。
五、莫比乌斯函数(mu)
对于一个数d,有:
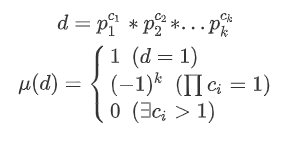
mu就是莫比乌斯函数。
换句话说就是:为1则函数值为1,,每个质因子只出现一次且质因子个数为奇数则为-1,为偶数则为1;出现了不止一次则为0.
这个函数是个积性函数。即:
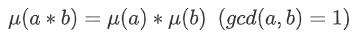
正确性显然,可以手动证明一下这9种情况。
考虑怎么线性求mu的值。同样可以利用积性函数的性质线筛质数来求。
见代码——
mu[1] = 1;//初始
for(int i = 2; i <= mx; i++) {
if(!in[i]) pri[++tot] = i, mu[i] = -1;//质数显然为-1
for(int j = 1; j <= tot && i * pri[j] <= mx; j++) {
register ll g = i * pri[j];
in[g] = true, mu[g] = mu[i] * mu[pri[j]];//积性函数
if(i % pri[j] == 0) {mu[g] = 0; break;}//不互质则质因子pri[j]出现多次,为0
}
}
讲一个莫比乌斯函数的常用性质:
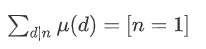
证明:考虑n的因数,mu不为0当且仅当为1或者选了一些质因子并且每个都只选了一次。考虑n有k个质因子,那就是:
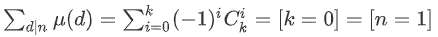
二项式定理可以证明。
还有一个性质是:
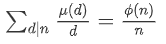
暂时不会证QvQ
六、莫比乌斯反演
莫比乌斯反演就是莫比乌斯函数的反演。公式为:

还有一个形式是:
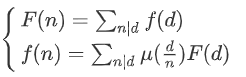
白嫖一下大佬翁小泽的博客证明:

到这里理论基础就差不多了。
其实一般普通的莫反不会考这么难,公式熟悉就好。
说白了就是我菜。
下面放一个例题吧:洛谷P3455?[POI2007]ZAP-Queries

这就是一个经典题。显然是求:
![\sum_{i=1}^a\sum_{j=1}^b[gcd(i,j)=d]](http://style.iis7.com/uploads/2021/09/14441073516.gif)
用上莫比乌斯函数的那个常用性质,可以转化为:
![\sum_{i=1}^{\frac{a}{d}}\sum_{j=1}^{\frac{b}{d}}[gcd(i, j)=1] =\sum_{i=1}^{\frac{a}{d}}\sum_{j=1}^{\frac{b}{d}}\sum_{x|gcd(i,j)}\mu(x)](http://style.iis7.com/uploads/2021/09/14441073517.gif)
套用莫比乌斯反演把mu提前,则相当于求有多少对i和j在a/d和b/d内并且gcd为x的倍数。

到这里就差不多了。如果Oa求肯定不行,多组询问。这里就可以用到整除分块了,对a/d和b/d整除分块,复杂度优化成根号的。
上代码——
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<map>
#define maxn 50004
using namespace std;
typedef long long ll;
const int mx = 5e4;
int read() {
int x = 0, f = 1, ch = getchar();
while(!isdigit(ch)) {if(ch == '-') f = -1; ch = getchar();}
while(isdigit(ch)) x = (x << 1) + (x << 3) + ch - '0', ch = getchar();
return x * f;
}
int pri[maxn], tot = 0, mu[maxn];
bool in[maxn];
int T, sum[maxn];
ll slv(int n, int m) {
if(n > m) swap(n, m);
register int l = 1, r; ll ans = 0;
while(l <= n) {
r = min(n / (n / l), m / (m / l));//两个上界取min,因为较小者的整除值变动了。
ans += 1ll * (sum[r] - sum[l - 1]) * (n / l) * (m / l);
l = r + 1;
}
return ans;
}
signed main() {
mu[1] = 1;//线筛莫比乌斯函数
for(int i = 2; i <= mx; i++) {
if(!in[i]) pri[++tot] = i, mu[i] = -1;
for(int j = 1; j <= tot && i * pri[j] <= mx; j++) {
register ll g = i * pri[j];
in[g] = true, mu[g] = -mu[i];
if(i % pri[j] == 0) {mu[g] = 0; break;}
}
}
for(int i = 1; i <= mx; i++) sum[i] = sum[i - 1] + mu[i];//前缀和
T = read();
while(T--) {
register int a = read(), b = read(), d = read();
printf("%lld\n", slv(a / d, b / d));//整除分块
}
return 0;
}
差不多是这样了。整理完了【除了某些证不来的东西QvQ
迎评:)
——End——
?
cs


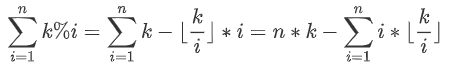
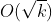 。
。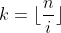 。则:
。则:
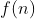 为积性函数,则满足:
为积性函数,则满足: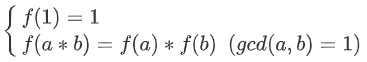


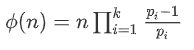
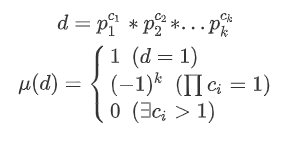

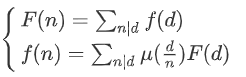


![\sum_{i=1}^a\sum_{j=1}^b[gcd(i,j)=d]](http://style.iis7.com/uploads/2021/09/14441073516.gif)
![\sum_{i=1}^{\frac{a}{d}}\sum_{j=1}^{\frac{b}{d}}[gcd(i, j)=1] =\sum_{i=1}^{\frac{a}{d}}\sum_{j=1}^{\frac{b}{d}}\sum_{x|gcd(i,j)}\mu(x)](http://style.iis7.com/uploads/2021/09/14441073517.gif)

